Tri- und Tetrahex — Spielsteine
Durch Zusammenfügen von 3 regelmäßigen Sechsecken (= Hexagone = Waben) erhält man Trihexe. Die Tetrahexe bestehen aus 4 verbundenen Hexagonen.
Es gibt 3 Tri- und 7 Tetrahexe. Sie gehören zur Familie der Polyhexe.

Puzzles aus Tri- und Tetrahexen
Es gibt nur 3 regelmäßige Polygone ( Vielecke mit gleichlangen Seiten und gleichen Innenwinkeln), mit denen man eine Fläche parkettieren kann: das Quadrat, das gleichseitige Dreieck und das regelmäßige Sechseck. So wie aus dem Quadrat und dem gleichseitigen Dreieck die Legespiele Pentomino und Hexiamond abgeleitet wurden, liegt es nahe durch Zusammenfügen mehrerer regelmäßiger Sechsecke ein entsprechendes Spiel aus Polywaben zu konstruieren.
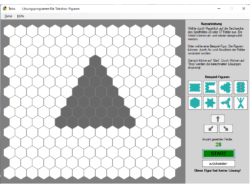
Die 7 Tetrahex-Steine ergeben eine Fläche von 28 Sechsecken, ergänzt man die Spielsteine um die 3 Trihexe sind es 37 Waben. Auf der Figurenübersichtsseite findet man einige Figuren, die man mit den Tetrahexen legen kann. Das zugrunde liegende Wabengitter lässt 6 Spiegelsymmetrien und 6 Drehsymmetrien zu. Beschränkt man sich auf die 7 Tetrahexe, existiert kein Figur mit maximaler Symmetrie, auch das abgebildete gleichseitige Dreieck hat keine Lösung. Erweitert man den Steine-Satz um die 3 Trihexe, so gibt es 2 Figuren — das Hexagon und die Schneeflocke — mit maximaler Symmetrie.