Polyformen
Der Begriff Polyform wird auf dieser Webseite in einem sehr allgemeinen Sinne verwendet und bezieht sich auf die Puzzleteile, die aus einfachen geometrischen Körpern zusammengesetzt sind. Polyformen können sowohl zweidimensionale als auch dreidimensionale Objekte sein und aus einer einzelnen Grundform oder verschiedenen Grundformen bestehen.
In der Regel fügen sich die Polyformen in ein Gitter ein, das die Art und Weise bestimmt, wie die Grundformen miteinander verbunden sind, und die möglichen Symmetrien der Figuren festlegt, die aus den zusammengesetzten Puzzleteilen entstehen.
Übersicht über die Polyformen dieser Webseite
zweidimensionale Polyformen
zweidimensionale Polyformen
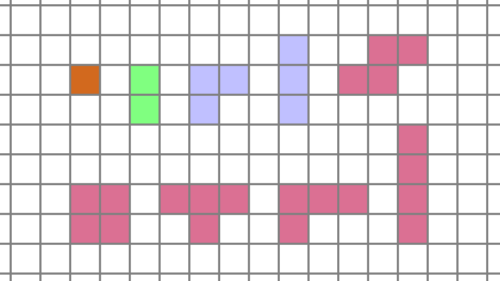
Polyominos
Polyominos sind Figuren aus identischen Quadraten, die mindestens eine Seite gemeinsam haben.
Es gibt:
1 Domino, 2 Triominos, 5 Tetrominos, 12 Pentominos, 35 Hexominos, 108 Heptominos, 369 Oktominos
Polyominos auf dieser Webseite:
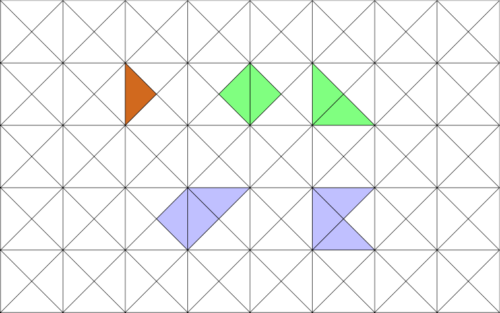
Polyamonds
Polyamonds sind Figuren aus gleichseitigen Dreiecken, die mindestens eine Seite gemeinsam haben
Es gibt:
1 Diamond, 1 Triamond, 3 Tetriamonds, 4 Pentiamonds, 12 Hexiamonds, 24 Heptiamonds, 66 Oktiamonds
Polyamonds auf dieser Webseite:
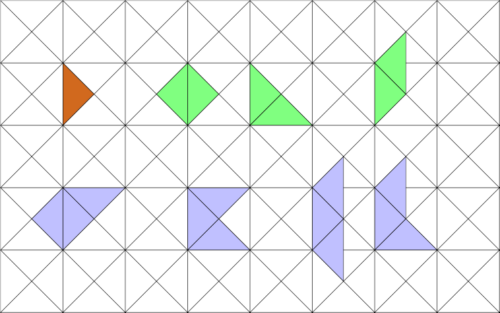
Polyabolos, Polytans
Polyabolos (andere Namen sind Polytans oder Supertangrams) sind Figuren aus gleichschenklig rechtwinkligen Dreiecken, die mindestens eine Seite gemeinsam haben. Die sich berührenden Seiten müssen entweder beides Katheten oder beides Hypotenusen sein.
Es gibt:
3 Diabolos, 4 Triabolos, 14 Tetrabolos, 30 Pentabolos, 107 Hexabolos, 318 Heptabolos, 1106 Oktobolos
Wenn man zusätzlich verlangt, dass die Polytans sich in das Tan-Gitter einfügen, so erhält man:
2 Ditans, 2 Tritans, 6 Tetratans, 8 Pentatans, 22 Hexatans, 42 Heptatans, 112 Oktotans
Polyabolos auf dieser Webseite:
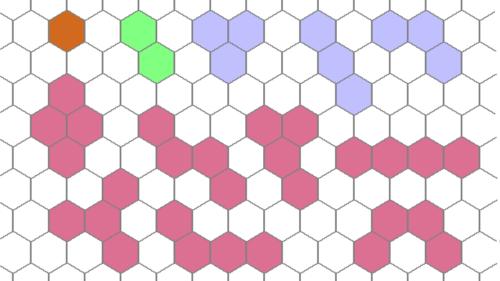
Polyhexe
Polyhexe sind Figuren aus regelmäßigen Sechsecken (Hexagons), die mindestens eine Seite gemeinsam haben.
Es gibt:
1 Dihex, 3 Trihexe, 7 Tetrahexe, 22 Pentahexe, 82 Hexahexe, 333 Heptahexe, 1448 Octahexe
Polyhexe auf dieser Webseite:
Polysplitcairos
Durch Halbieren eines Monocairo erhält man ein Monosplitcairo. Ein Monosplitcairo ist ein Viereck mit zwei gegenüberliegenden rechten Winkeln. Polysplitcairos passen in das abgebildete Gitter.
Es gibt:
Es gibt 3 Displitcairos, 6 Trisplitcairos, 22 Tetrasplitcairos, 63 Pentasplitcairos, 224 Hexaspitcairos, 760 Heptasplitcairos
Polysplitcairos auf dieser Webseite:
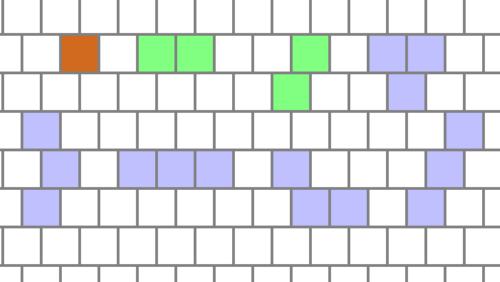
Polyhopse
Polyhopse sind Figuren aus identischen Quadraten. Beim zugrunde liegenden Gitter sind benachbarte Zeilen um jeweils ein halbes Quadrat versetzt.
Es gibt:
2 Dihopse, 5 Trihopse, 16 Tetrahopse, 55 Pentahopse, 225 Hexahopse, 949 Heptahopse, 4269 Octahopse
Polyhopse auf dieser Webseite:
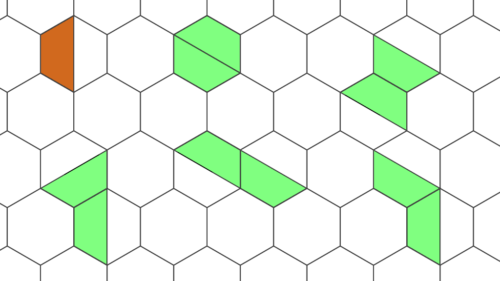
Polyhalbhexe
Polyhalbhexe sind Figuren aus halben Waben, die in das oben abgebildete Wabengitter passen.
Es gibt:
5 Dihalbhexe, 15 Trihalbhexe, 82 Tetrahalbehexe, 429 Pentahalbhexe
Polyhalbhexe auf dieser Webseite:
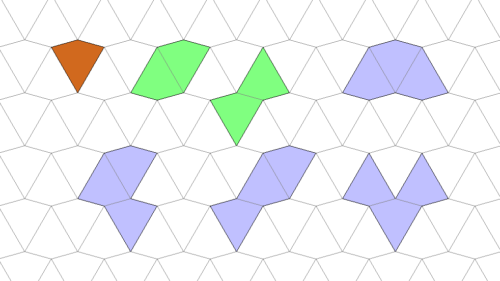
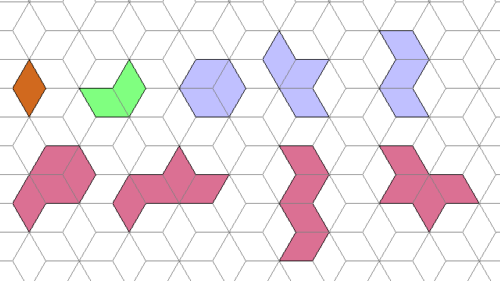
Polypons
Polypons sind Figuren aus Dreiecken mit zwei 30°-Winkeln, die in das oben abgebildete Gitter passen.
Es gibt:
2 Dipons, 2 Tripons, 4 Tetrapons, 4 Pentapons, 10 Hexapons, 13 Heptapons, 29 Octapons
Polypons auf dieser Webseite:
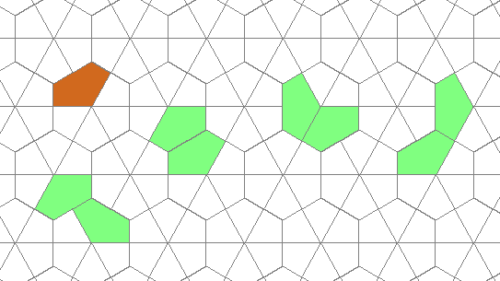
Polygeme
Polygeme sind Figuren aus Fünfecken, die aus einem Drittel eines regelmäßigen Sechsecks bestehen und in das oben abgebildete Gitter passen.
Es gibt:
4 Digeme, 15 Trigeme, 78 Tetrageme, 450 Pentageme, 2876 Hexageme, 18792 Heptageme
Polygeme auf dieser Webseite:
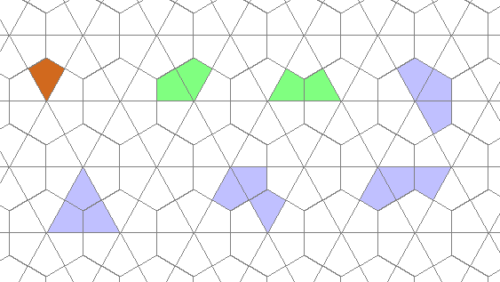
Polykites Typ 1
Polykites vom Typ 1 sind Figuren aus Drachenvierecken, die aus einem Sechstel eines regelmäßigen Sechsecks gebildet werden und in das oben abgebildete Gitter passen.
Es gibt:
2 Dikites, 4 Trikites, 10 Tetrakites, 27 Pentakites, 85 Hexakites, 262 Heptakites, 873 Octakites
Polykites auf dieser Webseite:
Polykites Typ 2
Polykites vom Typ 2 sind Figuren aus Drachenvierecken, die in das oben abgebildete Gitter passen.
Es gibt:
2 Dikites, 4 Trikites, 13 Tetrakites, 34 Pentakites, 120 Hexakites
Polykites auf dieser Webseite:
Polyzoide
Polyzoide sind Figuren aus Vierecken, die aus einem Viertel eines regelmäßigen Sechsecks bestehen, die in das oben abgebildete Gitter passen.
Es gibt:
7 Dizoide, 24 Trizoide, 147 Tetrazoide, 839 Pentazoide, 5461 Hexazoide
Polyzoide auf dieser Webseite:
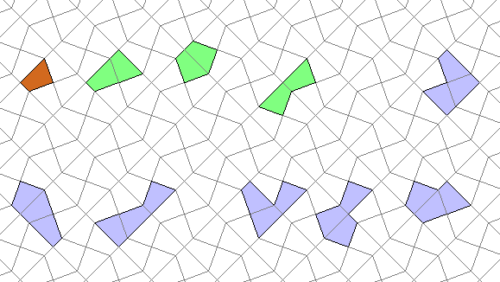
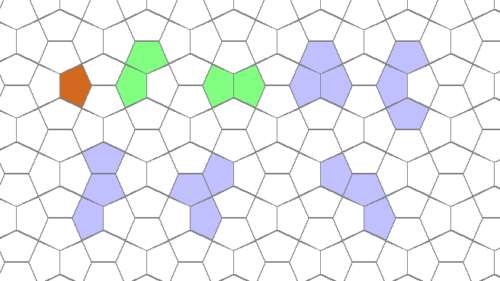
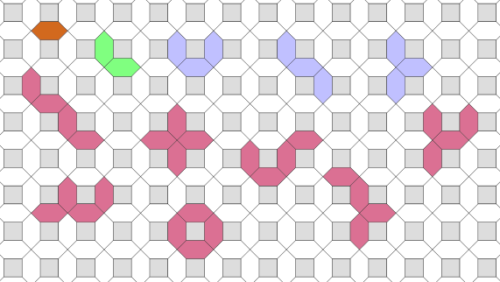
Polycairos
Polycairos sind Figuren aus Fünfecken, mit 2 rechten Winkeln, die in das oben abgebildete Gitter passen.
Es gibt:
2 Dicairos, 5 Tricairos, 17 Tetracairos, 55 Pentacairos, 206 Hexacairos, 781 Heptacairos, 3099 Octacairos
Polycairos auf dieser Webseite:
Polycubits
Die Grundform der Polycubits ist eine Raute mit zwei 60°-Winkeln und zwei 120°-Winkeln. Polycubits passen in das abgebildete Gitter.
Es gibt:
Es gibt 1 Dicubit, 3 Tricubits, 4 Tetracubits, 12 Pentacubits, 27 Hexacubits, 78 Heptacubits
Polycubits auf dieser Webseite:
Polyrhomben
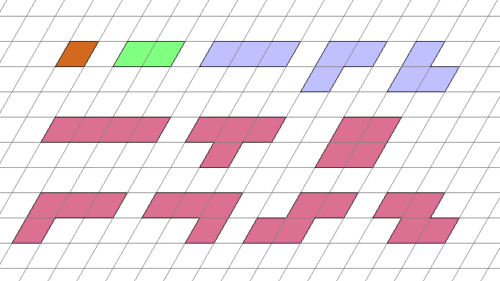
Die Polyrhomben bestehen aus Rauten, die im abgebildeten rhombischen Gitter angeordnet sind. Im Gegensatz zu den Polycubits müssen die Winkel der Rauten nicht 60° bzw. 120° betragen.
Es gibt:
1 Dirhombus, 3 Trirhomben, 7 Tetrarhomben, 20 Pentarhomben, 62 Hexarhomben, 204 Heptarhomben
Polyrhomben auf dieser Webseite:
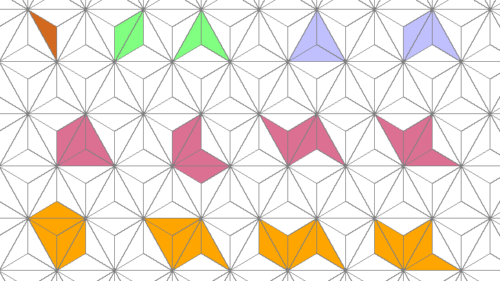
Polydrafter
Ein Monodrafter oder kurz Drafter ist ein Dreieck mit den Innenwinkeln 30°, 60° und 90°. Es können verschiedene Sets von Polydraftern gebildet werden, die von der Art des Zusammenfügens der Drafter und vom zugrundeliegenden Gitter abhängen.
Verbindung der Drafter
Eine häufig gestellte Bedingung, um aus einer zweidimensionalen Grundform Polyformen zu erhalten, ist, dass sich zwei Grundformen an ihrer gesamten Seitenlänge verbinden. Da bei den Draftern die kürzere der beiden Katheten halb so lang ist wie die Hypotenuse, kann man die Bedingung zum Zusammenfügen von Draftern so verändern, dass es auch erlaubt ist, dass nur eine Hälfte der Seitenlänge einer Hypotenuse verbunden ist.
Unter dieser Bedingung erhält man 13 Didrafter, 88 Tridrafter und 1041 Tetradrafter.
Gitterbedingung
Die Sets der Polydrafter können durch die Anforderung, dass sie sich in ein Gitter einfügen, also “gitterkonform” verhalten, verkleinert werden. Dabei kann entweder ein Gitter aus gleichseitigen Dreiecken oder das Draftergitter verwendet werden.
Für Polydrafter im Dreiecksgitter ergeben sich 6 Didrafter, 14 Tridrafter, 64 Tetradrafter, 237 Pentadrafter, 1025 Hexadrafter.
Für Polydrafter im Draftergitter ergeben sich 3 Didrafter, 3 Tridrafter, 9 Tetradrafter, 14 Pentadrafter, 38 Hexadrafter.
Polydrafter auf dieser Webseite:
Polyhextane
Ein Hextan ist ein Sechseck, dass man aus 6 rechtwinlig gleichseitigen Dreiecken bilden kann. Polyhextane passen in das abgebildete Lochgitter.
Es gibt:
Es gibt 1 Dihextan, 3 Trihextane, 7 Tetrahextane, 20 Pentahextane, 60 Hexahextane, 204 Heptahextane
Polyhextane auf dieser Webseite:
Nonagone
Das Nonagon-Gitter besteht aus regelmäßigen, 6‑strahligen Sternen und regelmäßigen Neunecken.
Nonagone auf dieser Webseite:
TriHexe
Das Trihex-Gitter besteht aus regelmäßigen Sechsecken und gleichseitigen Dreiecken
Trihexe auf dieser Webseite:
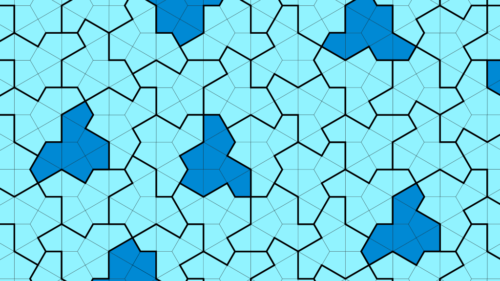
The Hat
“The Hat” oder “Einstein” besteht aus 8 Drachenvierecken. Er parkettiert die Ebene aperiodisch. Dies bedeutet, dass man durch Zusammenfügen von Einstein-Kacheln kein Muster erzeugen kann, das einfach kopiert, verschoben und eingefügt werden kann und die gesamte Ebene füllt.
Dennoch fügt sich die Kachel in ein hexagonales Gitter ein. Und es existieren symmetrische Figuren, die sich mit der Monofliese legen lassen. Um die Ebene zu parkettieren, wird die Monofliese beidseitig verwendet.
The Hat auf dieser Webseite:
Snubsquares
Das Snubsquare-Gitter besteht aus Quadraten und gleichseitigen Dreiecken im Verhältnis 1:2
Snubsquares auf dieser Webseite:
OctaPentas
Das OctaPenta-Gitter besteht aus regelmäßigen Achtecken und Pentagonen im Verhältnis 1:4.
Octapentas sind aus Octagonen und Pentagonen zusammengesetzt. Die Verbindung eines Octagons mit den Pentagons kann auf unterschiedliche Arten erfolgen:
- mit 2 Pentagons gibt es 6 Möglichkeiten
- mit 3 Pentagons gibt es 7 Möglichkeiten
- mit 4 Pentagons gibt es 13 Möglichkeiten
- mit 5 Pentagons gibt es 7 Möglichkeiten
- mit 6 Pentagons gibt es 6 Möglichkeiten
OctaPentas auf dieser Webseite:
BevelledSquares
Das BevelledSquare-Gitter besteht aus Quadraten und Sechsecken
BevelledSquares auf dieser Webseite:
dreidimensionale Polyformen
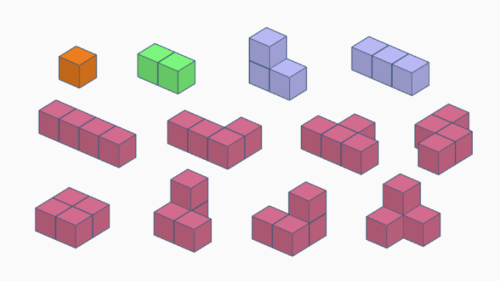
Polykuben
Polykuben oder Polywürfel sind Figuren aus zusammenhängenden Würfeln.
Es gibt:
1 Dikubus, 2 Trikuben, 8 Tetrakuben, 29 Pentakuben, 166 Hexakuben, 1023 Heptakuben, 6922 Octakuben
Polykuben auf dieser Webseite:
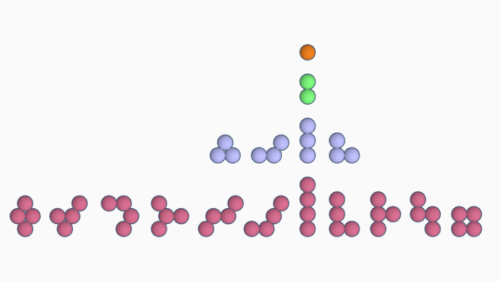
Polykugeln
Polykugeln sind Figuren aus sich berührenden Kugeln. Kugeln können in verschiedenen Gitterstrukturen platziert werden. Hier sollen nur das Tetraeder- bzw. Pyramidengitter betrachtet werden. Das Tetraedergitter und das Pyramidengitter sind identische Strukturen unterschiedlicher Perspektive.
Weiterhin beschränke ich mich hier auf die ebenen Polykugeln. Von den ebenen Polykugeln gibt es:
1 Dikugel, 4 Trikugeln, 11 Tetrakugeln, 33 Pentakugeln.
Polykugeln auf dieser Webseite:
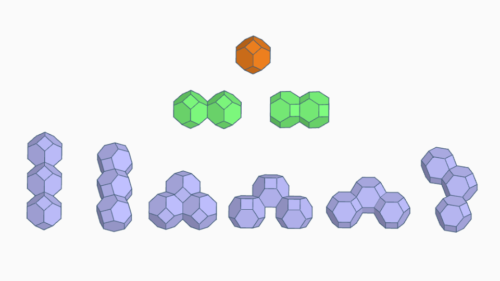
Polytrocs
Polytrocs sind Figuren aus Oktaederstümpfen. Sie füllen den Raum ohne Löcher.
Es gibt:
2 Ditrocs, 6 Tritrocs, 44 Tetratrocs, 394 Pentatrocs, 4680 Hexatrocs.
Polytrocs auf dieser Webseite:
Polyrhone
Polyrhone sind Figuren aus rhombischen Dodekaedern. Sie füllen den Raum ohne Löcher.
Es gibt:
1 Dirhon, 5 Trirhone, 28 Tetrarhone, 225 Pentarhone, 2274 Hexarhone.
Polyrhone auf dieser Webseite:
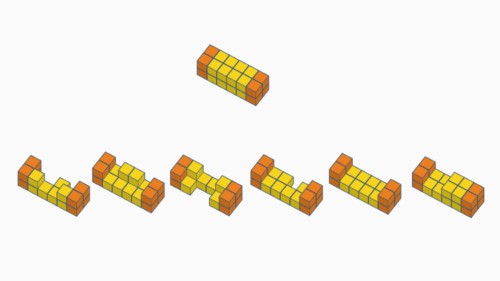
Knoten
Die 6‑teiligen Knoten-Puzzles bestehen aus 6 quadratischen Stäben. Jeden Stab kann man sich aus 24 Würfeln zusammengesetzt vorstellen. Die äußeren (orangenen) Würfel sind in allen Stäben vorhanden, einige der inneren (gelben) Würfel sind entfernt.
Knoten auf dieser Webseite:
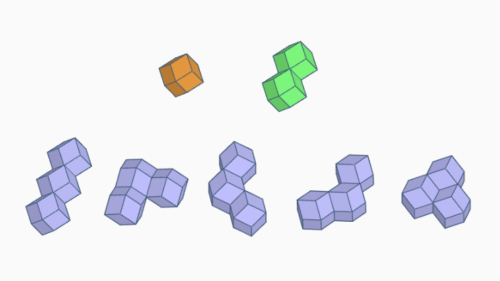
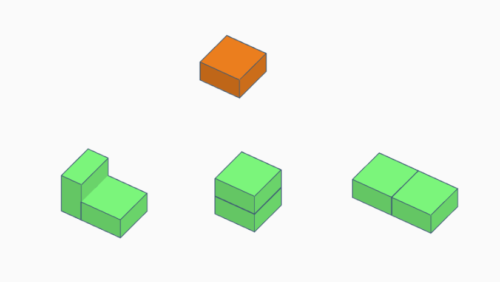
Polybes
Ein n‑Be ist ein Körper, der aus einem n‑Würfel entsteht, wenn die Hälfte jedes Würfels in einer solchen Weise entfernt wird, dass jeweils mindestens eine Verbindung mit halber Fläche erhalten bleibt.
Es gibt:
3 Dibes, 17 Tribes, 190 Tetrabes, 2190 Pentabes
Polybes auf dieser Webseite:
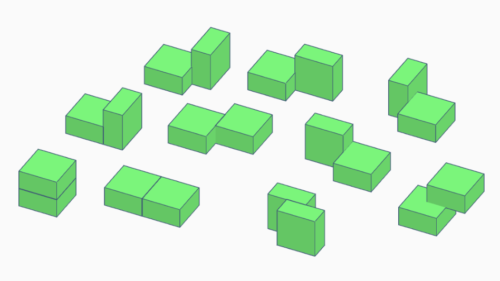
Gemini
Da mir kein Name bekannt ist, habe ich sie nach dem einzigen mir bekannten Spiel dieser Polyformen benannt.
Wie bei den Polybes ist die Grundform der Geminis die Hälfte eines Würfels. Bei den Geminis reicht es aber aus, wenn die Verbindung mindestens ein Viertel der Grundfläche beträgt.
Wenn man auf diese Weise zwei halbe Würfel verbindet, erhält man 10 verschiedene Formen.
Gemini auf dieser Webseite:
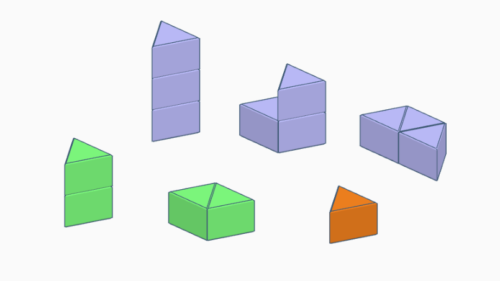
Polyamond-Prismen
Polyamond-Prismen sind Figuren aus regulären Dreiecksprismen (siehe auch Wikipedia). Ein solches Prisma erhält man durch Extrusion eines gleichseitigen Dreiecks (Moniamond).
Es gibt:
2 Diamond-Prismen, 3 Triamond-Prismen
Polyamond-Prismen auf dieser Webseite:
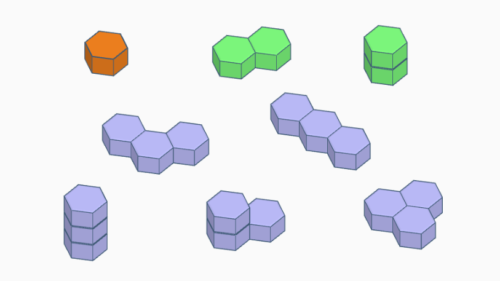
Polyhex-Prismen
Polyhex-Prismen sind Figuren aus regulären Sechseckprismen (siehe auch Wikipedia). Ein solches Prisma erhält man durch Extrusion eines gleichseitigen Sechsecks (Monohex).
Es gibt:
2 Dihex-Prismen, 5 Trihex-Prismen, 23 Tetrahex-Prismen
Polyhex-Prismen auf dieser Webseite:
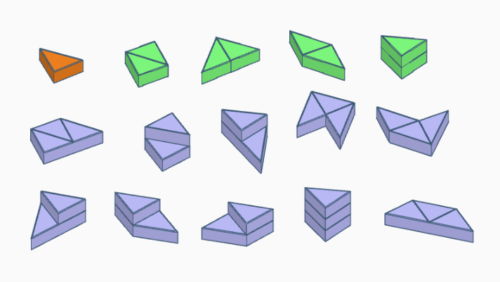
Polytan-Prismen
Polytan-Prismen sind Figuren aus rechtwinklig gleichschenkligen Dreiecksprismen (siehe auch Wikipedia). Ein solches Prisma erhält man durch Extrusion eines rechtwinklig gleichschenkligen Dreiecks (Monotan oder Monabolo).
Es gibt:
4 Ditan-Prismen, 10 Tritan-Prismen, 66 Tetratan-Prismen
Polytan-Prismen auf dieser Webseite:
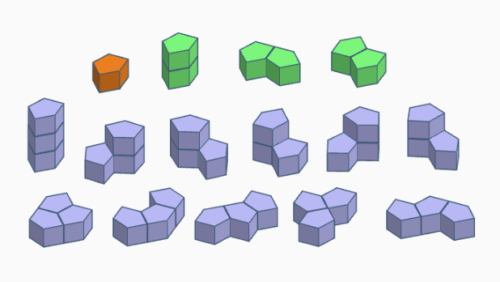
PolyCairo-Prismen
Polycairo-Prismen sind Figuren aus Monocairoprismen (siehe auch Wikipedia). Ein solches Prisma erhält man durch Extrusion eines MonoCairos.
Es gibt:
3 DiCairo-Prismen und 11 TriCairo-Prismen
PolyCairo-Prismen auf dieser Webseite:
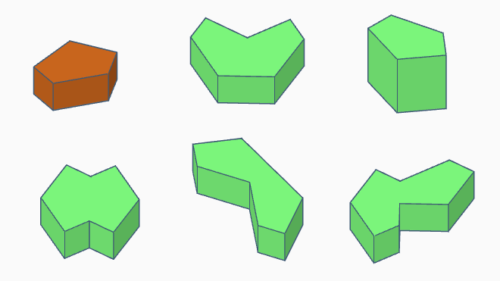
Polygem-Prismen
Polygem-Prismen sind Figuren aus Monogemprismen (siehe auch Wikipedia). Ein solches Prisma erhält man durch Extrusion eines Monogems.
Es gibt:
5 Digem-Prismen und 25 Trigem-Prismen
Polygem-Prismen auf dieser Webseite:
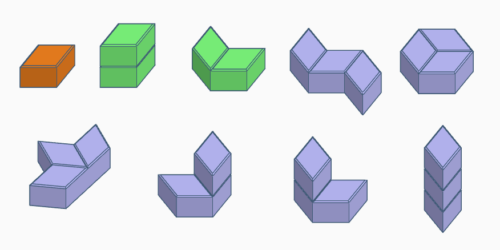
PolyCubit-Prismen
Ein regelmäßiges Sechseck lässt sich in 3 Rauten mit 60°- bwz. 120°-Innenwinkeln aufteilen. Extrudiert man die Rauten erhält man Rautenprismen.
Verbindet man Rautenprismen so, dass sie sich in das Cubitprismagitter einfügen, erhält man Polycubitprismen.
Es gibt:
2 DiCubitPrismen, 6 TriCubitPrismen und 24 TetraCubitPrismen