die Tangram — Spielsteine
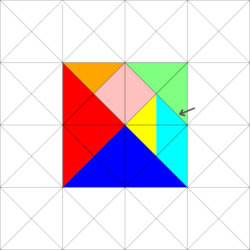
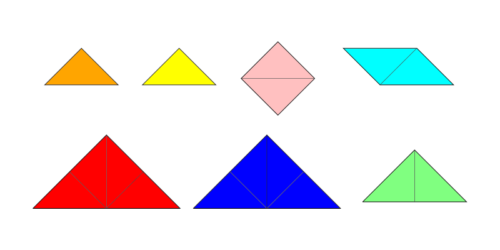
Das alte chinesische Legespiel Tangram ist wohl das bekannteste der hier vorgestellten Spiele. Es besteht aus 7 Puzzleteilen verschiedener Größe und Form.
Die Grundform der Spielsteine ist ein gleichseitig rechtwinkliges Dreieck. Die Puzzleteile gehören damit zur Familie der Polytans (=Polyabolos). Die beiden kleinen Dreiecke bestehen aus einem, das mittlere Dreieck, das Quadrat und das Parallelogramm bestehen aus je zwei und die beiden großen Dreiecke aus je vier Dreiecken.
Das Tangram als Puzzle
Woher bekommt man ein Tangram-Puzzle?
Das Tangram-Spiel wird in Versionen aus Holz oder Pappe im Handel angeboten. Man kann es aber leicht selbst herstellen. Dazu genügt bereits eine Schere und ein Blatt Papier. Im Download-Bereich dieser Webseite stehen Bastelvorlagen für ein Puzzle aus Pappe und Vorlagen für den 3D-Drucker zum Herunterladen bereit.
Auf der Figurenübersichtsseite sind einige Tangram-Figuren abgebildet. Im Downloadbereich lassen sich für diese Figuren Figurenvorlagen, die sowohl für die Papp- als auch die 3D gedruckten Tangrams passen, herunterladen.
Figuren und Lösungsprogramm
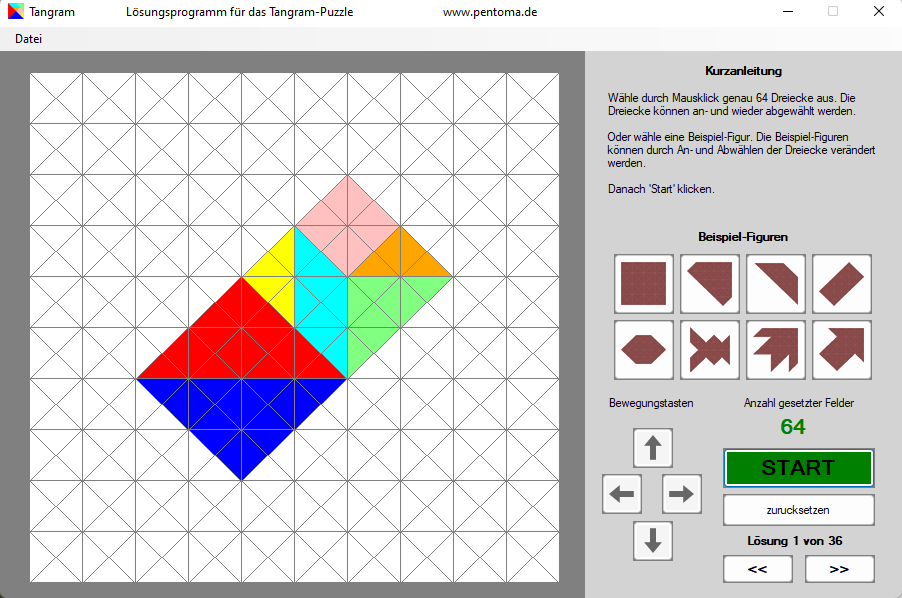
Es gibt tausende verschiedener Figuren für das Tangram. Einige (wenige) von ihnen, wie zum Beispiel das Quadrat, lassen sich in ein Gitter aus gleichseitig rechtwinkligen Dreiecken einpassen. Man muss dabei aber das Gitter so fein wählen, dass das kleine Tangram-Dreieck aus 4 Dreiecken gebildet wird, da andernfalls die meisten Lösungen nicht “gitterkonform” sind, das bedeutet, dass die Figur insgesamt sich in das Gitter einfügt, jedoch einzelne Spielsteine Gittergrenzen nicht einhalten.
Für Figuren, die in ein Gitter passen, gibt es auf der Downloadseite ein Lösungsprogramm für Tangram-Figuren.
Konvexe Figuren
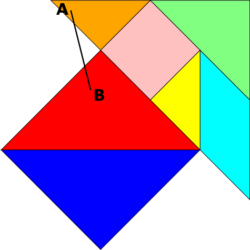
Defintion:
Eine geometrische Figur heißt genau dann konvex, wenn mit zwei beliebigen Punkten A und B der Figur auch die gesamte Verbindungsstrecke von A und B zur Figur gehört.
Für das Tangram-Puzzle gibt es nur 13 konvexe Figuren (Beweis: Fu Traing Wang und Chuan-Chih Hsiung 1942). Alle konvexen Figuren sind gitterkonform.