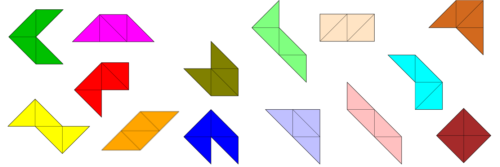
Tetrabolo — Spielsteine
Die 14 Tetrabolos sind aus je 4 gleichschenklig rechtwinkligen Dreiecken zusammengesetzt. Die Dreiecke berühren sich jeweils entweder an ihren Hypothenusen oder an ihren Katheten (also nicht Hypothenuse an Kathete). Die Tetrabolos gehören zur Familie der Polyabolos (ein anderer Name ist Polytans).
Tetrabolo — Puzzles
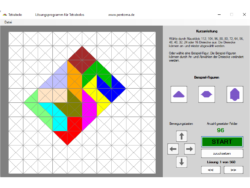
Martin Gardner hat die Tetrabolos in seinem Buch „Mathematische Hexereien“ vorgestellt. 14 Tetrabolos ergeben eine Fläche von 56 Dreiecken. Das zugrundeliegende Gitter aus gleichseitig rechtwinkligen Dreiecken lässt 4‑fach drehsymmetrische Figuren mit 4 Spiegelachsen zu. Figuren mit maximaler Symmetrie, die aus allen 14 Tetrabolos bestehen, existieren aber nicht. Auch das abgebildete Rechteck hat keine Lösung. Die wenigen symmetrischen Figuren aus 14 Tetrabolos besitzen nur eine Spiegelachse.
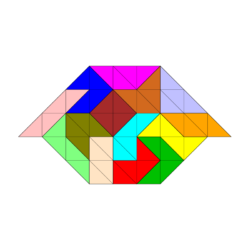
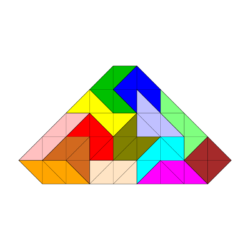
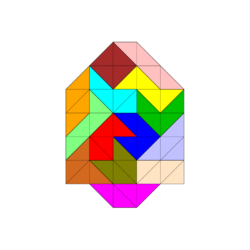
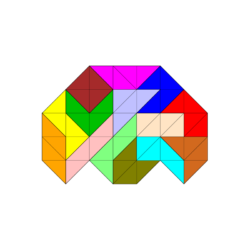
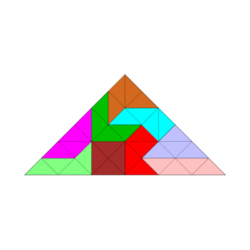
Für Figuren, die aus weniger als 14 Spielsteinen bestehen, sieht es, was die Symmetrien angeht, besser aus. Die Abbildungen zeigen vollsymmetrische und rechteckige Figuren.
Einige weitere Tetrabolo-Figuren